York Maths tutor - GCSE Maths Revision
York Maths tutor has prepared help sheets below helping students to solve 5 common questions many students have problems with. All help sheets can be viewed online using the links below:
Help Sheet 1 - Prime Factorisation:
Problem: How to factorise a number into a product of its primes
Solution: DRAW A FACTOR TREE!
Example 1: Give the prime factorisation of 120.
Solution: All we need to do is to break 120 down into any known factors (it doesn't matter which you choose).
We know that 120 = 12 x 10, so let's start the factor tree:

Now 12 and 10 are NOT prime numbers so we need to break them down further. We know that 12 = 4 x 3
and 10 = 5 x 2, so let's add these to the tree:

The numbers 3; 5 and 2 ARE prime numbers! We cannot break them down further and so we circle
these on the diagram; this is important.
Remember to circle the prime numbers.
Finally, we know that 4 = 2 x 2 and so we can now complete the tree:

To get the prime factorisation, we just need to MULTIPLY all the circled numbers together:
120 = 3 x 5 x 2 x 2 x 2 = 3 x 5 x 23.
And so the prime factorisation of 120 is 3 x 5 x 23.
Help Sheet 2 - Highest Common Factor (HCF):
Problem: How to find the highest common factor of two numbers.
Solution: DRAW A FACTOR TREE!
Example 1: Find the highest common factor of 120 and 160.
Solution: Let's start by drawing both factor trees:
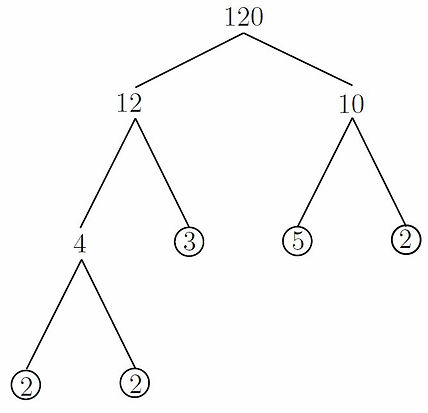
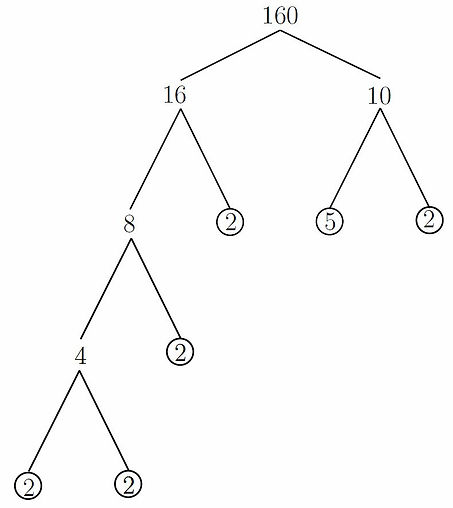
Using the factor trees we know that the prime factorisations of 120 and 160 are:
120 = 5 x 3 x 2^3
160 = 5 x 2^5
Now we are looking for the highest common factor between the two numbers. We can see that both 120 and 160 have a common factor of 5 and 2^3.
To get the highest common factor, we just multiply the common prime factors together to get 5 x 2^3 = 40.
And so the highest common factor of 120 and 160 is 40.
Help Sheet 3 - Lowest Common Multiple (LCM):
Problem: How to find the LCM of two numbers.
Solution: DRAW THE FACTOR TREES!
Example 1: Find the LCM of 120 and 160.
Solution: Let's start by drawing both factor trees:


Using the factor trees we know that the prime factorisations of 120 and 160 are:
120 = 5 x 3 x 2^3
160 = 5 x 2^5
Now we are looking for the lowest common multiple of the two numbers. To get the lowest common multiple
we multiply together the factors of HIGHEST power between the two factorisations.
We spot that both numbers have a factor of 5 so we will include this in our calculation. Now the highest
power of 3 between 120 and 160 is 3^1 in 120 (160 doesn't have a factor of 3), and so we will again include this
number in our calculation. Finally, 120 has a factor of 2^3 and 160 has a factor of 2^5. We take the highest
power of 2 which is 2^5 and include this in our calculation.
And so the LCM of 120 and 160 is 5 x 3 x 2^5 = 480.
Example 2: Find the LCM of 56, 30 and 450.
Solution: We find the prime factorisations (by drawing factor trees) to be:
56 = 7 x 2^3
30 = 5 x 3 x 2
450 = 5^2 x 3^2 x 2
Now we are looking for the lowest common multiple of the three numbers. To get the lowest common multiple we multiply together the factors of HIGHEST power between the three factorisations.
We spot that 56 has a factor of 7 so we will include this in our calculation. Now the highest power of 5
between 56, 30 and 450 is 5^2 and so we include this number in our calculation. Furthermore, we note that
the highest power of 3 between 56, 30 and 450 is 3^2, so we include this number in our calculation. Finally,
the highest power of 2 between the three numbers is 2^3 in 56; again, we will include this in our calculation.
And so the LCM of 56, 30 and 450 is 7 x 5^2 x 3^2 x 2^3 = 12600.
Help Sheet 4 - Recurring Decimals:
Problem: How to write recurring decimals as fractions. (non-calculator)
Solution: 3 Steps
Step 1: Set x equal to the decimal you want to turn into a fraction.
Step 2: Manipulate x in such a way that you can form two simultaneous equations which
cancel out the recurring part when added/subtracted.
Step 3: Solve the simultaneous equations.
Example 1: Write the number 0.3 ̇=0.333333333… as a fraction.
Solution:

The goal is to get rid of the recurring part by subtraction. Notice that 10x = 3:3333333333… We now
have two simultaneous equations:

We can see that when we subtract these two equations the recurring part will vanish. Doing (2) - (1) gives:
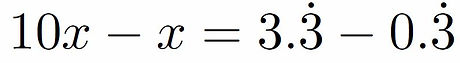
This simplifies to:

And we can rearrange the equation to make x the subject giving:

(You probably already knew that 0.3 ̇=1/3 but the above proves that this is the case)
Example 2: Convert 0.17 ̇2 ̇ to a fraction in its most simplified form.
Step 1:
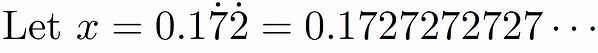
The goal is to get rid of the recurring part by subtraction. Let’s first try We now have two
simultaneous equations:

The problem is that these two equations do not cancel out the recurring part when subtracted. So let us
now try instead. This gives us two new simultaneous equations:

We can see now that the recurring part will vanish when we subtract the equations. Doing (6) - (5) gives:

This simplifies to:

And we can rearrange the equation to make x the subject giving:


Be careful! The question asked for the fraction in its most simplified form. Note that 990 = 9 x 110 and
171 = 9 x 19. Thus, we can simplify the fraction further 171/990=19/110.
And so the final answer is:
Help Sheet 5 - Factoring Quadratic Expressions:
Problem: How to factor a quadratic.
Solution: 3 Steps
Step 1: Factor out any common factors if it has any.
Step 2: If there are no common factors and a = 1 then use the product/sum method.
Step 3: If there are no common factors and a 6= 1 then use decomposition.
Example 1: Factorise

Solution: We follow step 1 first. Does the expression have any common factors? YES! Both terms contain
an x, so we pull the x out, giving the answer:

Example 2: Factorise
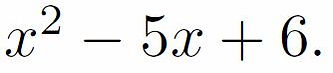
Solution: We follow step 1 first. Does the expression have any common factors? NO! so we need to use
another step.
Notice that the coefficient of x2 is 1 (a = 1) so this tells us that we need to use step 2.
Now we are looking for two numbers that multiply together to make 6 and add together to make -5.
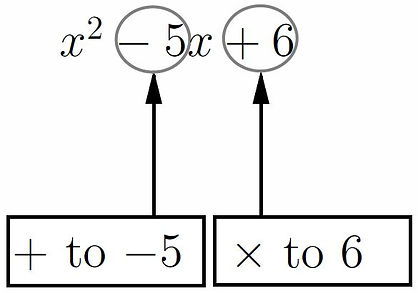
How many ways can we make 6 by multiplying together two integers? Let's list them. We could have:
These are the only options. Now let’s check which ones add to -5:
Now we can see that -3 - 2 = -5 and so we know that the numbers we need to put into the brackets are
-3 and -2. And so we have the answer:

Tip: check that your answer is correct by expanding out the brackets.
Example 3: Factorise

Solution: We follow step 1 first. Does the expression have any common factors? NO! so we need to use
another step.
Notice that the coefficient of x2 is 4 (a = 4) so this tells us that we need to use step 3: decomposition.
Now we are looking for two numbers that multiply together to make 8 and add together to make 6. We get
the number 8 by multiplying a and c together in ax2+bx+c. In this example a = 4, c = 2 and 4_2 = 8.

How many ways can we make 8 by multiplying together two integers? Let's list them. We could have:
These are the only options. Now let’s check which ones add to 6:
Now we can see that 4 + 2 = 6 and so we decompose the 6x term into 4x + 2x:
Now we have:

Which we group as (4x2 + 4x) + (2x + 2)
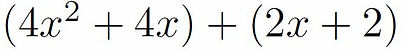
Now the first group has a common factor of 4x and the second group has a common factor of 2. We now
factorise these groups to give:

Notice that both terms now have a common factor of (x+1), so let's factor this out to give the final answer:

Tip: check that your answer is correct by expanding out the brackets.
